Understanding the Euler Number (e) Through Examples

The Euler number, denoted as $e$, is a fundamental constant in mathematics approximately equal to 2.71828. It's not just any number; it's the base of natural logarithms and plays a vital role in calculus, finance, and physics. Let's dive into some intriguing examples to see $e$ in action.

Compound Interest

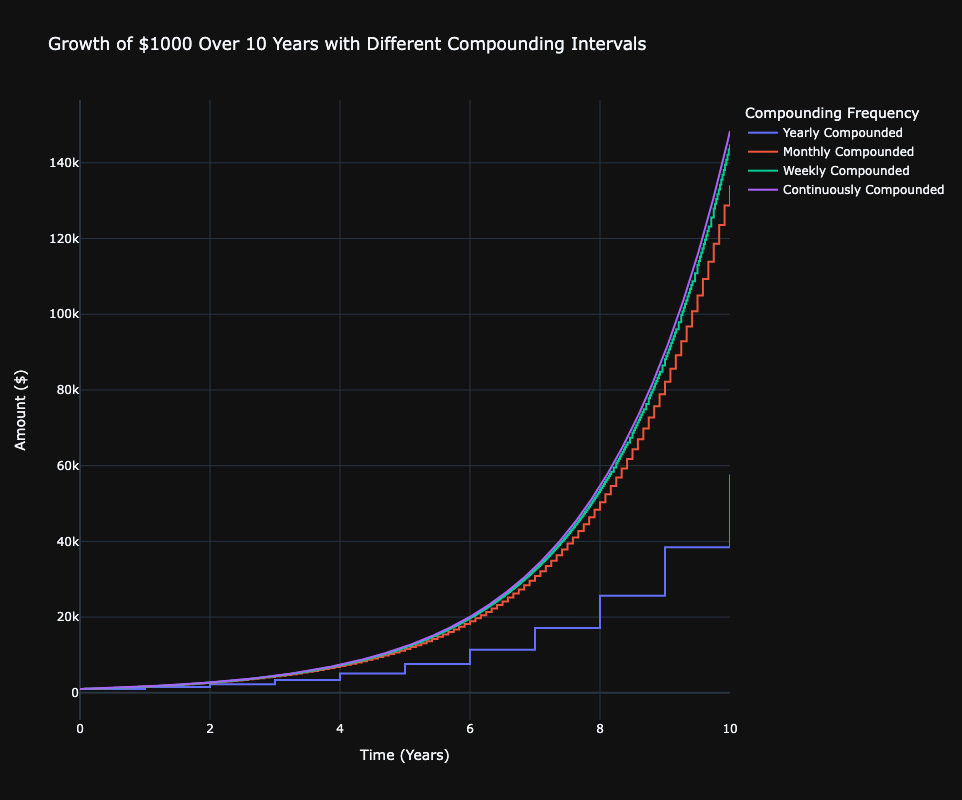
One of the most relatable examples of the Euler number is in calculating compound interest. Imagine you invest $1 at a 100% interest rate per year. If this interest is compounded annually, you'll end up with $2. But what if the interest is compounded more frequently, or even continuously?

The formula for continuous compounding is:

\[ A = Pe^{rt} \]

where:

$A$ is the amount of money accumulated after n years, including interest.
$P$ is the principal amount (the initial sum of money).
$r$ is the annual interest rate (in decimal).
$t$ is the time the money is invested for in years.

For continuous compounding, with $P = 1$, $r = 1$, and $t = 1$, we find that $A = e^1 = e$, showing that continuous compounding yields about $2.71828.

Exponential Growth and Decay

The Euler number also describes natural growth and decay processes. For example, the population of a species, the discharge of a capacitor, or the decay of a radioactive substance.

The formula for exponential growth or decay is:

\[ N(t) = N_0e^{rt} \]

where:

$N(t)$ is the quantity at time $t$.
$N_0$ is the initial quantity.
$r$ is the rate of growth (if positive) or decay (if negative).
$t$ is the time that has passed.

Jupyter Notebook

Continuing with the explanation of the Euler number, which is denoted as $e$, it holds a unique and pivotal role in mathematics, particularly in the context of exponential functions and calculus. The Euler number is approximately equal to 2.71828 and is the base of the natural logarithm. This number is not just a constant, but it also represents the rate of growth that is unparalleled in its efficiency and balance between growth and decay.

Euler's number value uniqness

When considering the function $y = e^x$, a few remarkable properties emerge, especially at $x = 1$:

Value of $y$: At $x = 1$, the value of $y$ becomes $e^1 = e$. This means that the function $y = e^x$ evaluates to the Euler number itself when $x = 1$. This is a fundamental property that showcases how $e$ serves as a natural growth rate.
Area Under the Curve: For the exponential function $y = e^x$, the area under the curve from $x = 0$ to $x = 1$ is exactly equal to $e$. This integral, $\int_0^1 e^x dx$, yields the value of $e - 1$, demonstrating the natural logarithmic base's intrinsic relationship with the concept of area under the curve in calculus.
Slope of the Curve: The derivative of $y = e^x$ with respect to $x$ is also $e^x$. This means that at $x = 1$, the slope of the curve is $e$. The function $y = e^x$ is unique in that the rate of change of the function at any point is equal to the value of the function at that point. This property is a cornerstone in differential equations and the study of growth processes.
Intercept: When $x = 0$, $y = e^0 = 1$. The curve of $y = e^x$ intersects the y-axis at $y = 1$, indicating that the growth process starts from a base value of 1 when considering natural growth phenomena.

The Euler number's special properties, such as the equality of the area under the curve to $e$ for $x = 1$, the fact that the slope of $y = e^x$ at $x = 1$ is $e$, and its natural emergence in various mathematical and real-world contexts, underscore its significance. It not only defines exponential growth and decay in the most natural way possible but also links various branches of mathematics, from calculus to complex analysis, in a coherent and elegant manner.

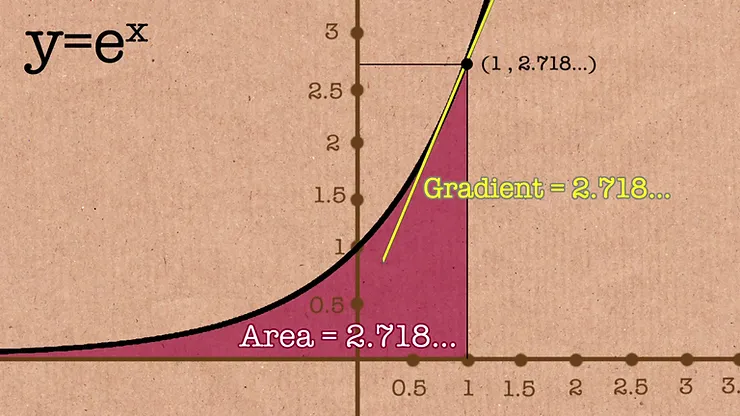
Image Credit: Numberphile

Euler's Formula in Complex Analysis

Euler's formula is a beautiful and profound connection between exponential functions and trigonometric functions, stated as:

\[ e^{ix} = \cos(x) + i\sin(x) \]

where $i$ is the imaginary unit. This formula demonstrates the deep relationship between trigonometry and exponential functions, particularly when $x = \pi$, leading to Euler's identity:

\[ e^{i\pi} + 1 = 0 \]

This identity elegantly links five fundamental mathematical constants: $e$, $i$, $\pi$, 1, and 0.

Conclusion

The Euler number $e$ is more than just a numerical constant; it's a bridge connecting various areas of mathematics, from finance to complex analysis. Its properties and the formulas it's part of are essential for students and professionals alike to understand the natural world and the abstract realms of mathematics.

For more visit 3b1b